
The rotate primitive combines rotations around the three main axis. Partial rotations are applied in their natural order: x, y, and then, z. If you need another order, you can combine independent rotations.
Rotations are very important for modeling, since several primitive shapes are always defined with a given orientation. For instance, the box shape is always axis-aligned.

The basic technique for specifying a rotation is using three consecutive rotations around the coordinate axis:
First, the object is rotated around the X axis, then, around the Y axis, and finally, around the Z axis. Consider this example:
rotate(-45, 45, 0,
cone(0, 0, 0, 3, 1, metal(forestGreen, 0.2)))The result is the same as the result of this variant:
rotate(0, 45, 0,
rotate(-45, 0, 0,
cone(0, 0, 0, 3, 1, metal(forestGreen, 0.2))))Since rotations are not commutative, this alternative order renders a diferent image:
rotate(-45, 0, 0,
rotate(0, 45, 0,
cone(0, 0, 0, 3, 1, metal(forestGreen, 0.2))))
The cone at the left corresponds to a X-rotation followed by a Y-rotation. The cone at the right was first rotated around the Y-axis, but cones has Y axis simmetry by default, and the rotation doesn't have any effect on it, so we only see the effect of the final X axis rotation.
The spin infix binary operator is the preferred way to rotate a shape:
cone(0, 0, 0, 3, 1, metal(forestGreen, 0.2)))
spin -45^X + 45^Y;By using spin instead of Rotate, you avoid a couple of parenthesis. Additionally, spin is a infix binary operator, so the shape to rotate appears now at the beginning of the expression, which is easier to read.
There's yet another variant for the spin operator syntax: the spin/around pair. Rotate always rotate shapes around the origin of coordinates. That's useful when defining a shape near this point, but it complicates things when the shape has already been moved to another location in the scene. Let's define a box for demonstrating this:
box(0, -2, -1, 2, 0, 1,
gradient(yellow, -2^y, springGreen, 2^y))We'll add three small spheres to identify three reference points in the X axis:
sphere( 0, 0, 0, 0.10, metal(red, 0.2)),
sphere(-1, 0, 0, 0.10, metal(darkOrange, 0.2)),
sphere(+1, 0, 0, 0.10, metal(darkOrange, 0.2));This is how our scene could render so far:
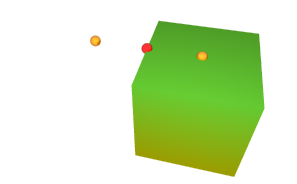
Now, we will rotate the box 45 degrees... and, since no around clause has been used yet, the rotation will be defined around the origin of coordinates:
box(0, -2, -1, 2, 0, 1,
gradient(yellow, -2^Y, springGreen, 2^Y))
spin 45^Y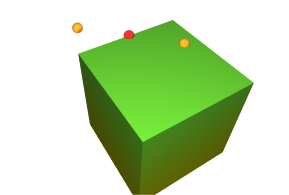
As you can check, the box has rotated around the Y, or vertical, axis: the small red sphere is still at the edge of the cube. This may be or may be not what you want. Now look this example:
box(0, -2, -1, 2, 0, 1,
gradient(yellow, -2^Y, springGreen, 2^Y))
spin 45^Y around [1,0,0]This time, there's is an around clause after the spin operator. And this is the rendered scene:
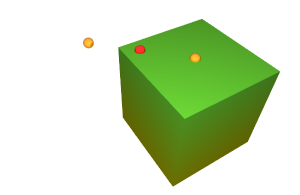
XSight RT handles the around clause by generating two translations, one before and the other after the rotation. The former moves the coordinates frame so the center of rotation matches the origin of coordinates.After the rotation, the frame is moved to its original location:
box(0, -2, -1, 2, 0, 1,
gradient(yellow, -2^Y, springGreen, 2^Y))
move [-1,0,0]
spin 45^Y
move [+1,0,0]The funny side of all this is that those translations are later simplified and vanish from the scene tree. After the simplification pass, our box would be defined like this:
box(-0.293, -2.000, -0.293, 1.707, 0.000, 1.707,
gradient(yellow, -2^Y, springGreen, 2^Y))
spin 45^YIf you have doubts about the order of rotations, you should use two cascading Rotate operations. This technique doesn't slow rendering, because both rotations are merged by the engine. Whenever possible, rotations are statically applied to shapes with simmetries.
Probably you are wondering why could anybody want to rotate a sphere with its center at the origin of coordinates. The answer spells object composition. Take a look at this scene:
 |
// The stuff pills are made of...
set PillStuff = Spotted(White, color(254, 254, 248), 15.0, 6, 0.05, 0.0, 0.0);
set Pill = Difference(
Cylinder(0, 0, 0, 0.2, 1.0, PillStuff),
Box(-0.1, 0.1, -1.2, 0.1, 0.3, 1.2, PillStuff),
PillStuff) |
Pills in the pile are rotated around the Y axis, and that implies a rotation of the difference between a cylinder and a box. But there's no need to rotate a cylinder. So, the rotation is moved down the scene tree to be applied only to the box.
Not all shapes have full rotation simmetry: actually, only the sphere does:
In all the above mentioned cases, a rotation can be eliminated from the scene. Some shapes are internally defined along with a transformation, as the cylinder and the cone. In these cases, the new rotation is merged with the internal transformation to accelerate rendering.
Finally, we have special shapes for handling some common cases in a more efficient manner:
You can check which equivalences has been used when optimizing a given scene by looking at the scene tree.
Home | Small Instantiation Language overview | SILLY predefined shapes | Transforms | Translate | Scale | CSG operations | Infinite surfaces